What are Algebra Tiles?
Algebra tiles are manipulatives used in mathematics. This math manipulative promotes inquiry based learning. These virtual math manipulatives can help students better understand algebraic concepts and definitions. The tiles can be used to teach a variety of concepts, including counting, area, perimeter, and arithmetic, as well as equations, factoring quadratics, algebraic long division, and simultaneous equations. Learn how to represent and solve algebraic problems using these virtual algebra tiles to represent variables and constants. Factor and expand equations, substitute variable expressions, and solve equations. By adding tiles, deleting zero sets, and modeling equations, students can go through algebra.
In this blog, we’ll look at a few algebra tiles examples of how Algebra tiles have been useful for teachers introducing this complex subject to students.
Counting
We introduce students to Algebra tiles at a young age by using them as simple counters, using only the small, square tile. We can ask students to use the tiles to represent a specific number or to count up or down from a certain starting number. This can be expanded to counting up or down in specific increments, such as “Here are 6 tiles; can you count up in twos until you have 10 tiles?”
Arithmetic
Algebra tiles can be used to teach the concept of equals sign. The equals sign can be introduced by establishing the rule that the number of tiles on both sides of the sign must always be the same. I recommend spending a lot of time with young children making number sentences like 4 = 4, 5 = 3 Plus 2, 7 = 10 – 3, and so on. It is impossible to ignore the significance of the equals sign.
Counting can be extended by adding and subtracting positive numbers. These virtual algebra tiles can be used to demonstrate how addition and subtraction work, as well as to give numbers and symbols in number sentences meaning.
Multiplication can be represented in a variety of ways through these math manipulatives, including arrays, areas, collections of groups, and so on.
Grouping, sharing, and repeated subtraction are all examples of division.
Negative number addition and subtraction involves the use of the reverse side of the tile, which is the first step in introducing the concept of Zero Pairs.
Zero Pairs
Zero Pairs is the most important concept in the use of Algebra Tiles. Many teachers want to get to using the tiles for algebraic expressions or equations as early as possible, so they don’t spend enough time establishing the notion of Zero Pairs. The effectiveness of using Algebra tiles is restricted unless this concept is well explained and understood.
The reverse of each positive tile is a red tile. The tile’s red face represents the tile’s negative. Combining a tile with its red counterpart would result in a total area of zero because the red tile has the same absolute dimensions and area as the yellow tile.
We may introduce addition and subtraction of integers using the Zero Pairs concept.
Add Algebraic Expressions
Let’s solve the following algebraic expression using algebra tiles.
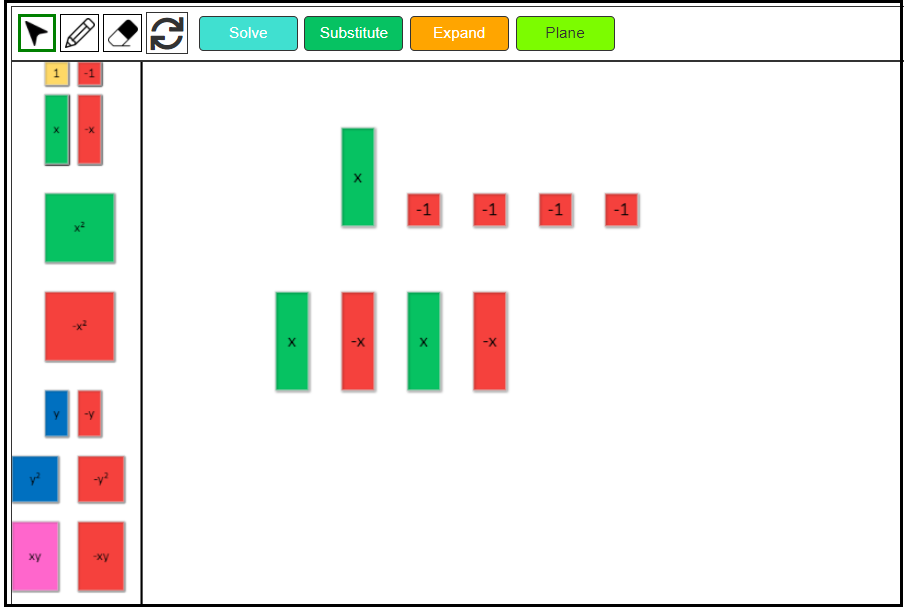
(3x – 4) + (-x + 1)
1. Model each linear expression.
To model each linear expression, drag the virtual algebra tile that represents the corresponding part of the expression.
First, model the expression 3x – 4. Drag 3 green positive x tiles and 4 negative 1-tiles.
Next, model the expression -x + 1. Drag 1 red negative x tile and 1 positive 1-tile.
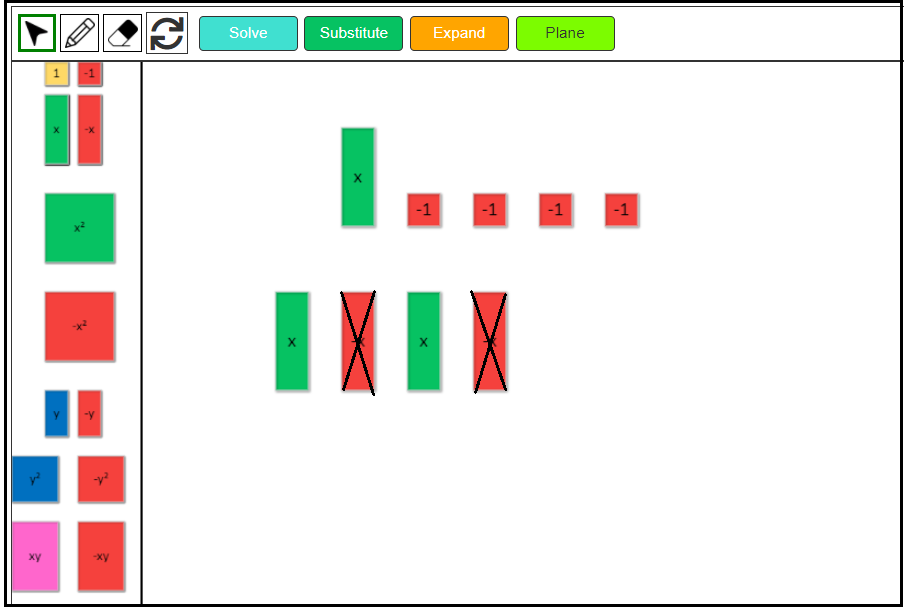
2. Remove all zero pairs.
Click on the eraser to remove all zero pairs. One positive x-tile will cancel one negative x-tile. Similarly, one negative 1-tile will cancel out one positive 1-tile.
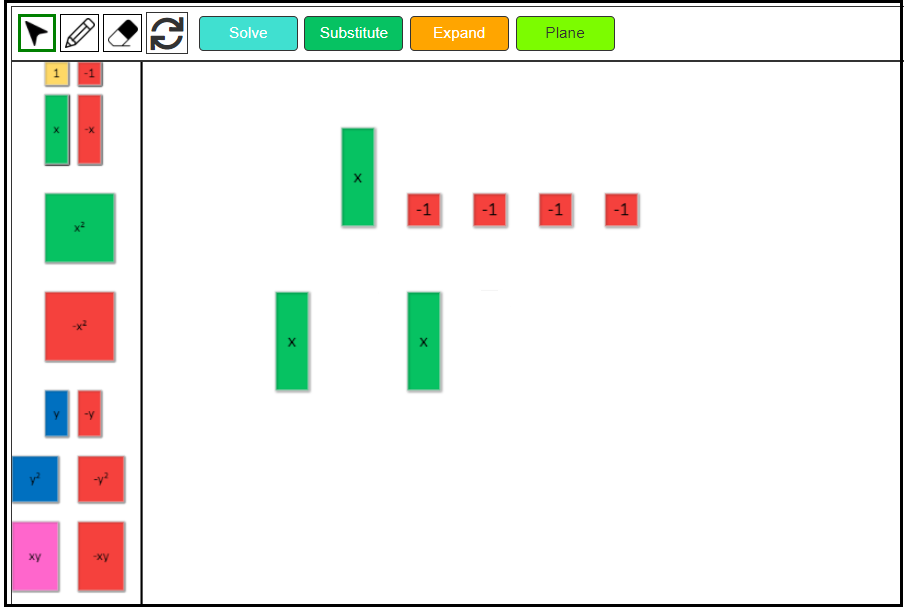
3. Write a linear expression for the remaining tiles.
We can see that we have two positive x-tiles and three negative 1-tiles remaining. Hence, the answer is -2x – 3.
Subtract Algebraic Expressions
Let’s solve the following algebraic expression using virtual algebra tiles.
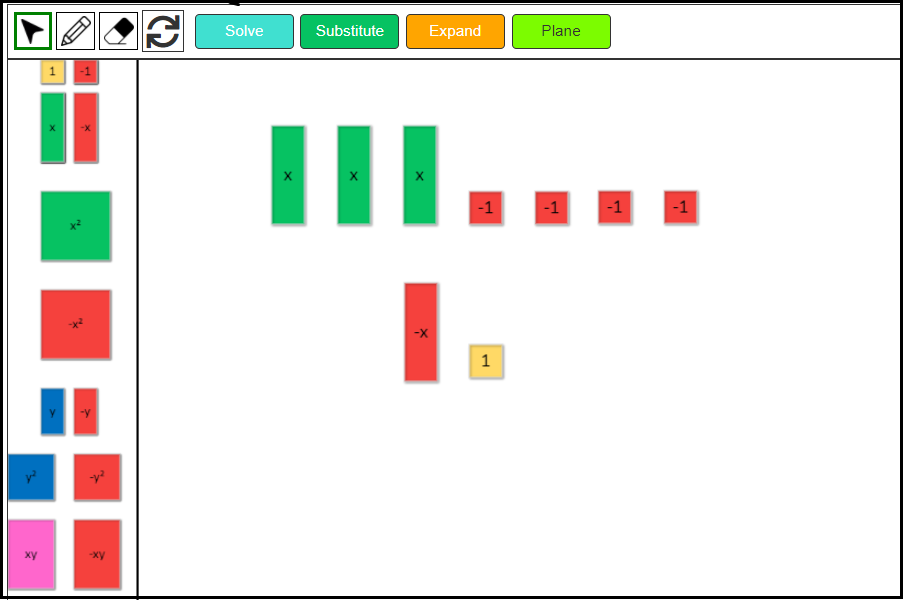
(x – 4) – (-2x + 1)
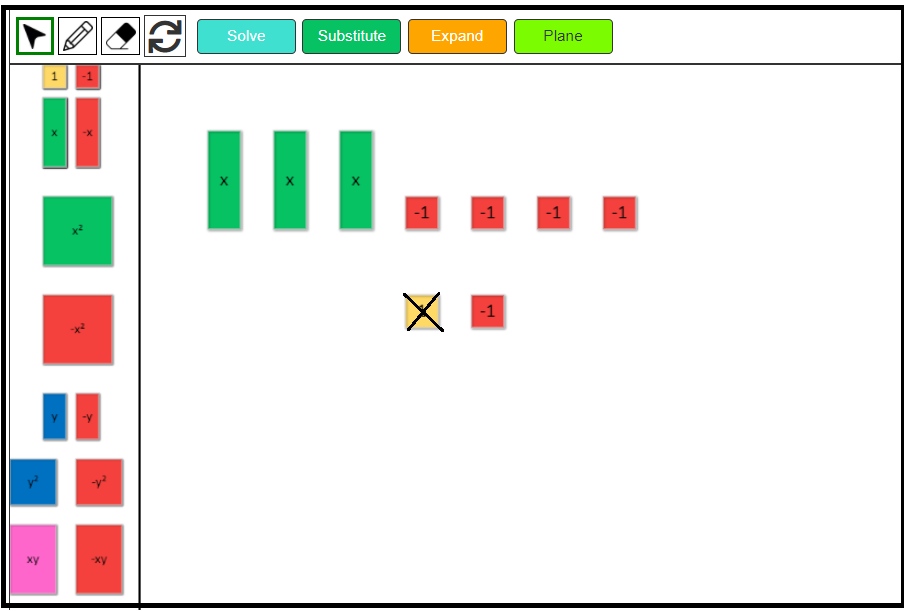
1. Model each linear expression.
First, model the expression x – 4. Drag 1 green positive x-tile and four negative 1-tiles.
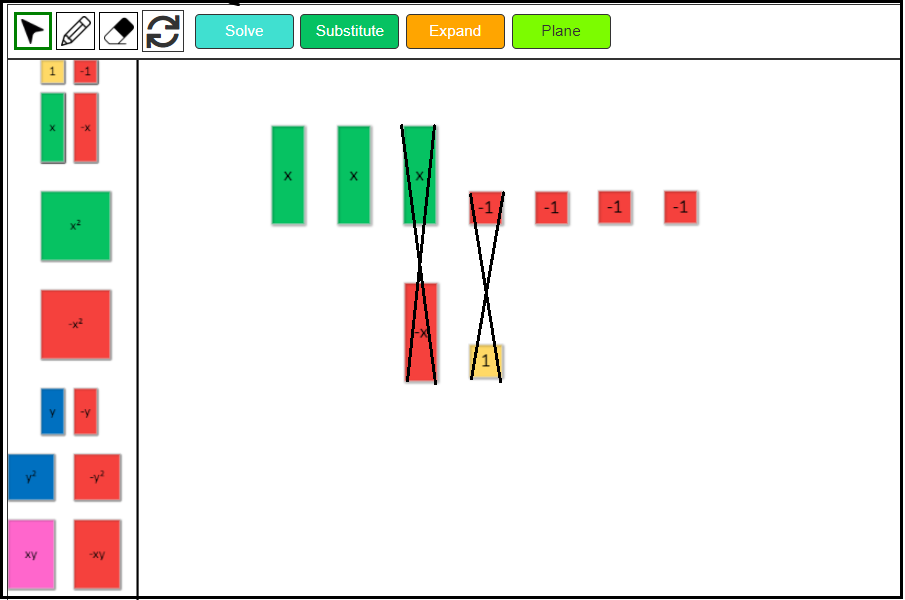
2. Add or remove zero pairs as needed to subtract.
We can see that there is 1 positive green x-tile, and we need to remove 2 negative x-tiles. As we don’t have any negative x-tile, we will have to add 2 zero pairs of x-tiles.
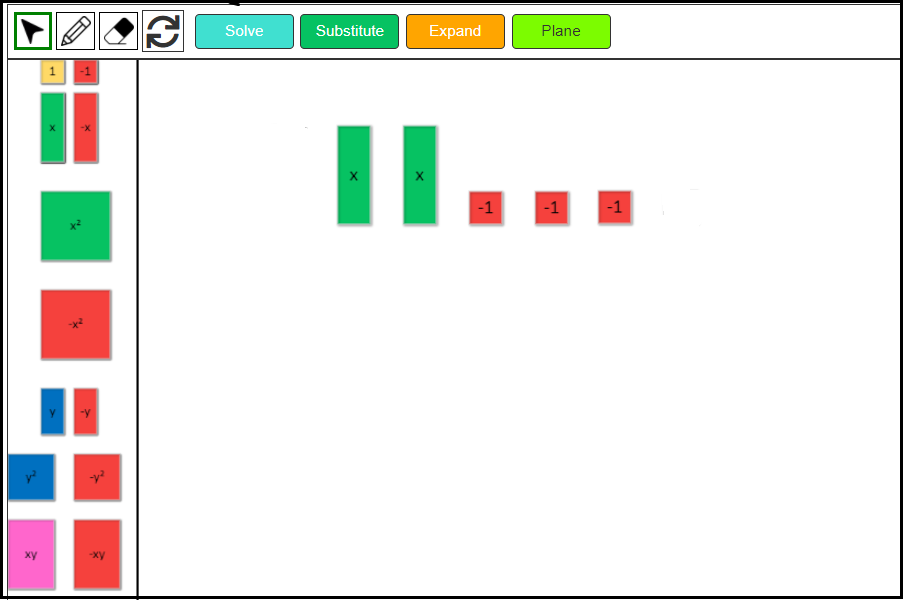
Next, click on the eraser to remove 2 negative x-tiles. We have 3 green positive x-tiles remaining.
We also have 4 negative 1-tiles, and we are asked to remove a positive 1-tile. As we don’t have any positive 1-tiles, we need to add a zero pair of 1-tiles. Now we can easily remove a positive 1-tile using the eraser. We have 5 negative 1-tiles remaining.
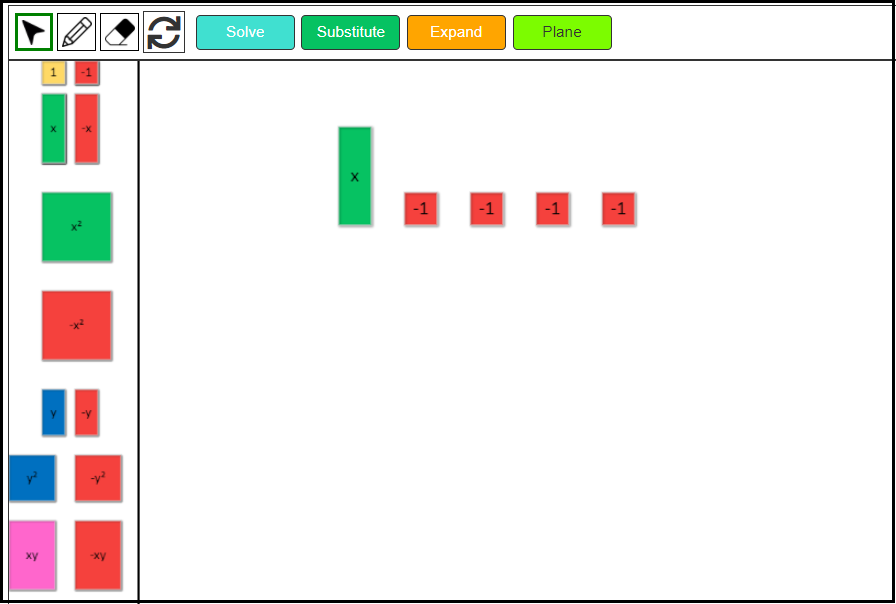
3. Write a linear expression for the remaining tiles.
We can see that we have 3 positive x-tiles and 5 negative 1-tiles remaining. Hence, the answer is 3x – 5.
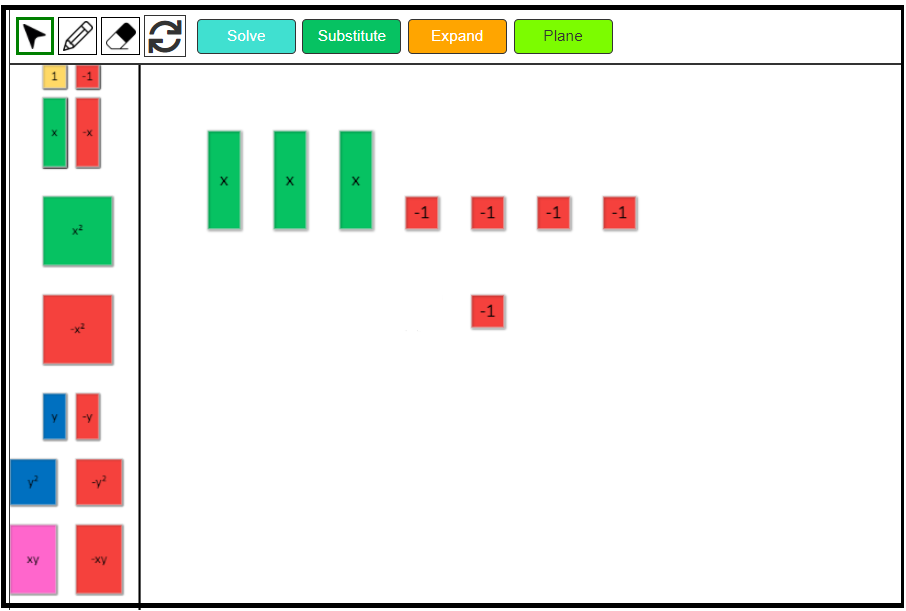
Divide Algebraic Equations
Let’s solve the following algebraic equation using algebra tiles digital math manipulative.
2x = 6
1. First, model the expression 2x = 6. Drag 2 green positive x tiles on the left side of the mat and 6 positive 1-tiles on the right side of the mat.
2. We have to find the value of one x-tile. In order to get x by itself, we have to split the x-tiles into 2 equal groups. We can easily split the x-tiles as shown. We now have 2 groups of 1x.
3. Similarly, split the six 1-tiles into 2 equal groups. We can easily split the 1-tiles as shown.
4. We can see that one group, or one x-tile equals three 1-tiles.
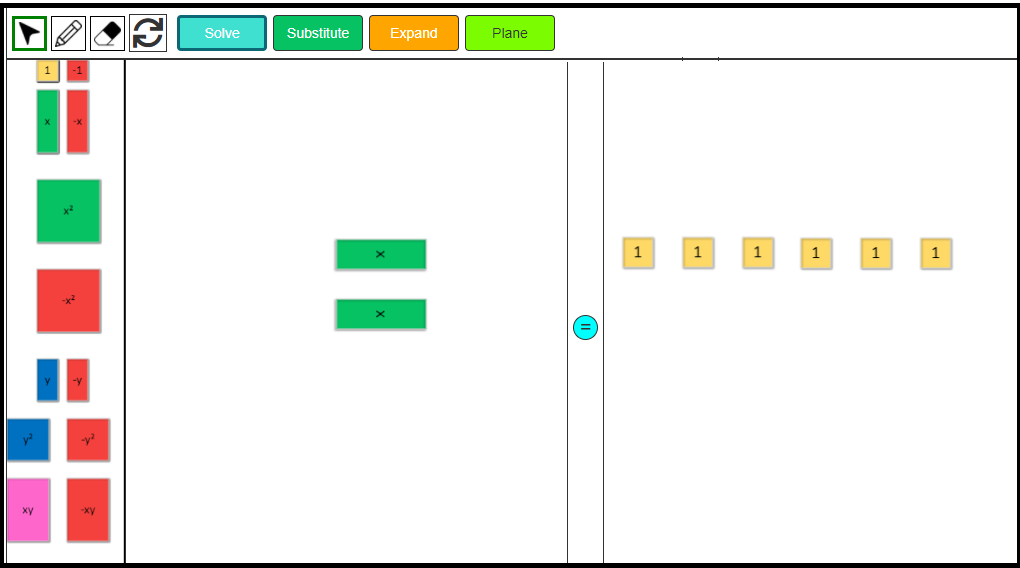
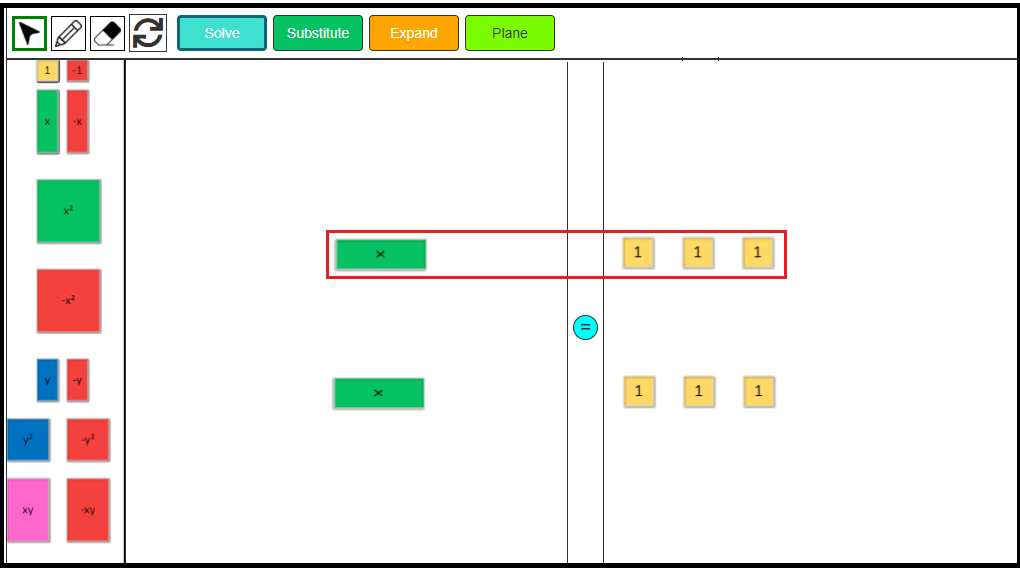
Substitute to Solve Algebraic Expressions
Let’s solve the following algebraic expression using these virtual algebra tiles.
x + 7 when x = 4
1. Click on the Substitute button to change the layout.
2. Drag one green x-tile and seven positive 1-tiles to model the expression x + 7 in the ‘Expression’ mat.
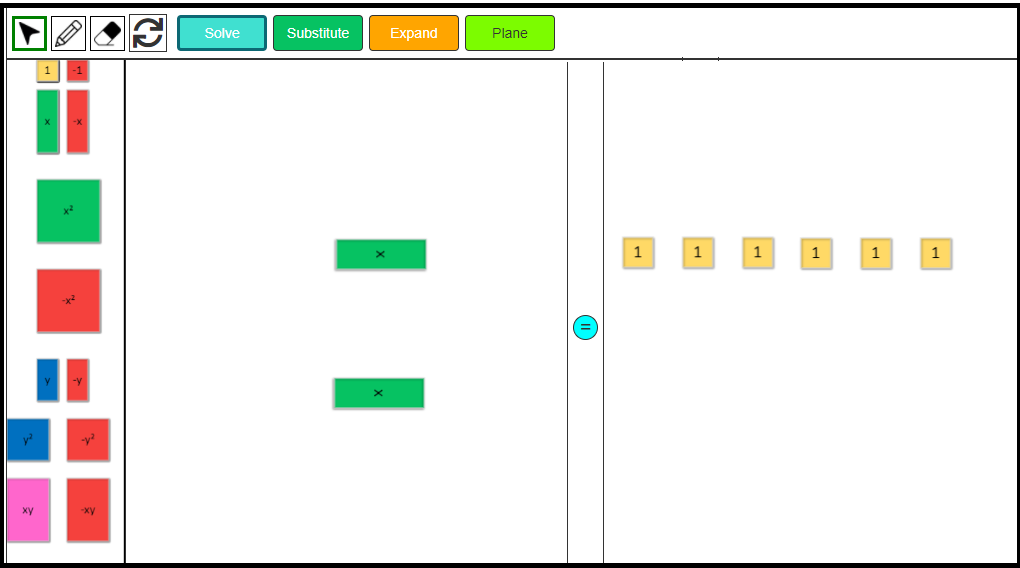
3. As the value of x is already given, drag one positive x tile on the left side of the mat and four positive green tiles on the right side of the mat. We need ‘substitute’ the value of x i.e. 4 in place of x.
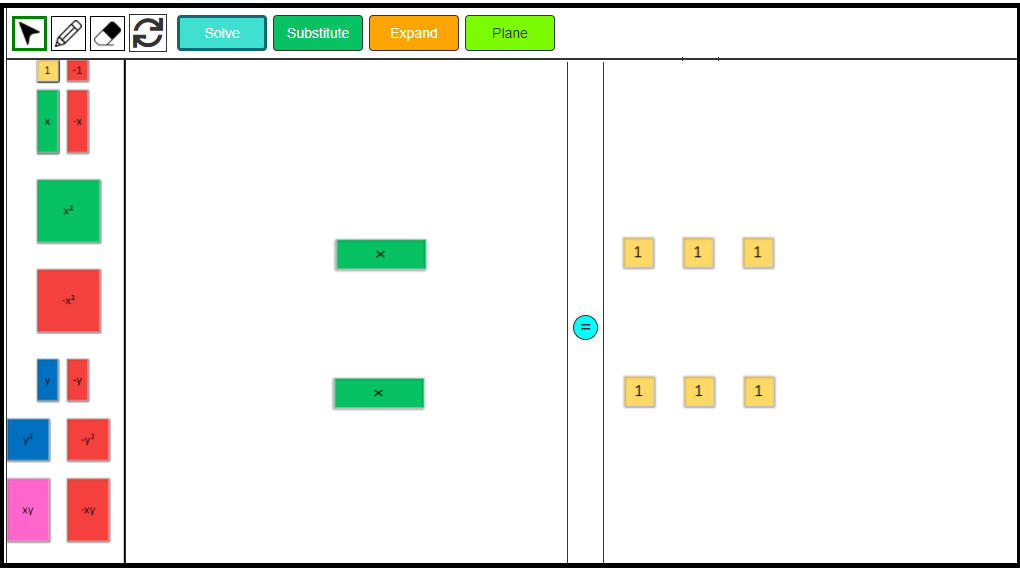
4. Drag the 4 positive 1-tiles to the x-tile on the expression mat to ‘replace’ or ‘substitute’ with the green x-tile. Use the eraser to remove the x-tile tile as it has now been replaced.
5. We now have 11 green 1-tiles. Hence the value of the expression x + 7, when x = 4, is 11.
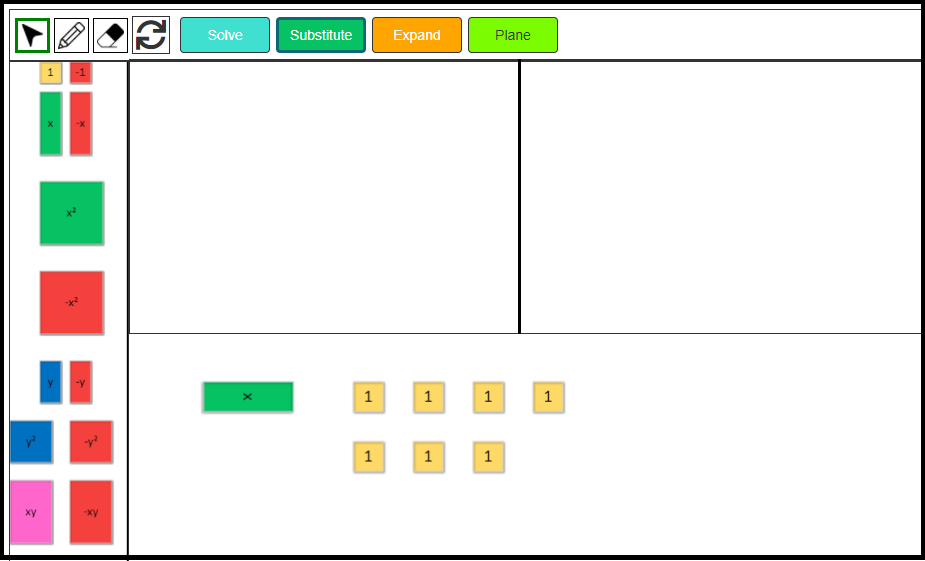
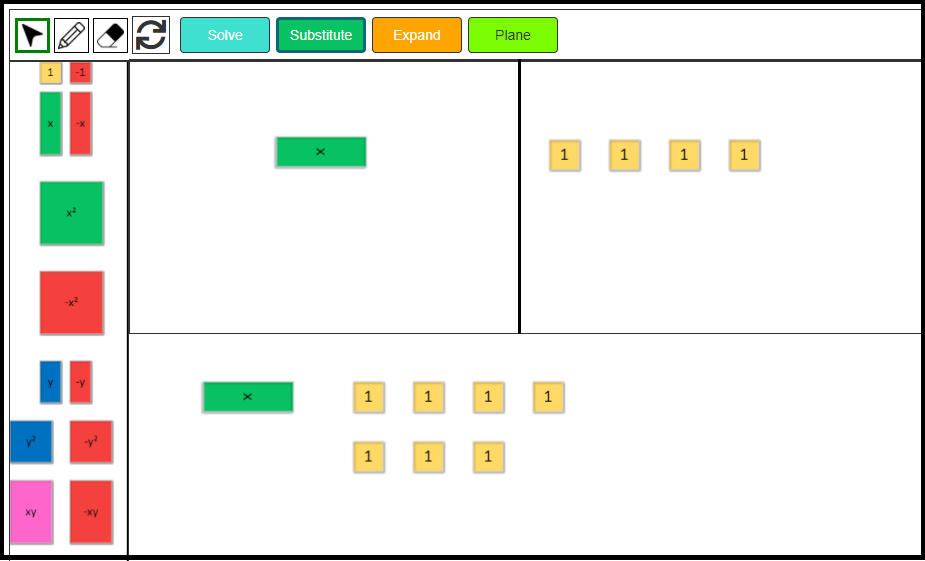
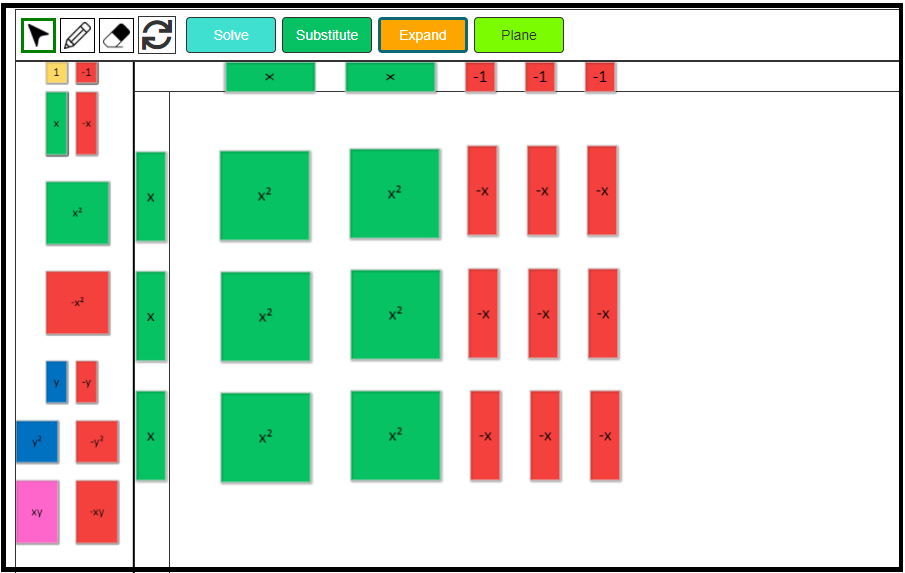
Expand Algebraic Expression
Let’s expand the following algebraic expression using algebra tiles.
3x(2x – 3)
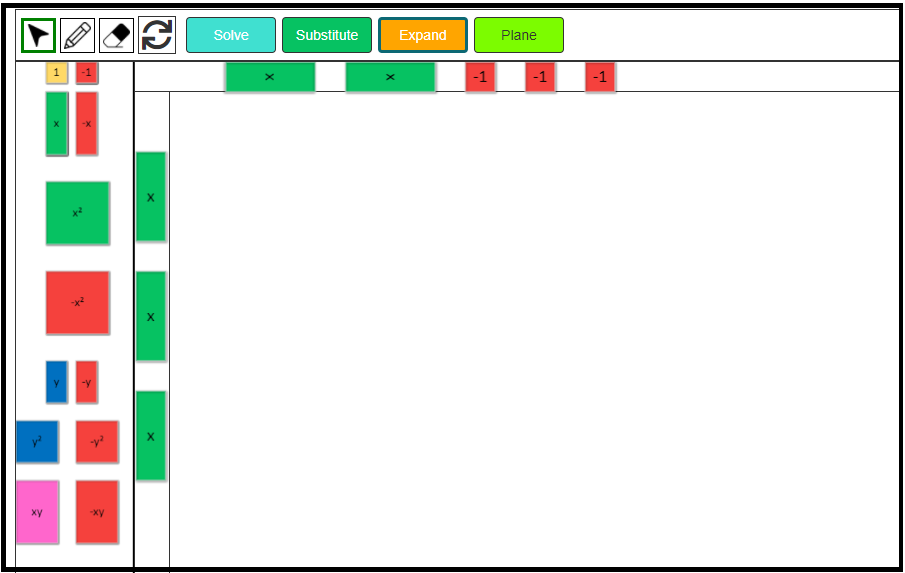
1. Click on the Expand button to change the layout.
2. Insert three green positive x-tiles to model 3x in the left side column. Insert two positive green x-tiles and three negative 1-tiles in the top row to model the expression 2x – 3.
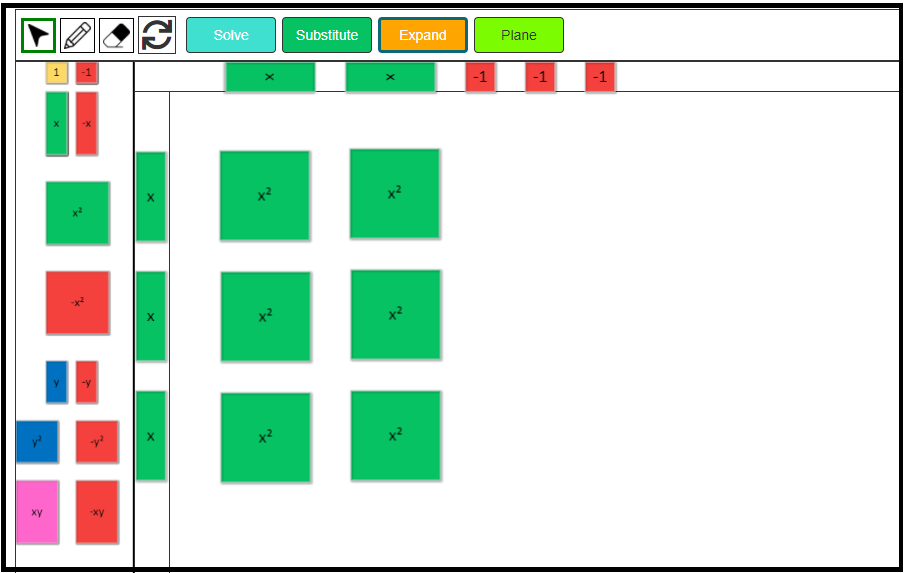
3. x times x is x2, so fill all the spaces with the positive x2 tiles.
4. x times -1 is -x, so fill all the remaining spaces with negative x tiles.
Hence, 3x(2x – 3) = 6x2 – 9x
Teachers will provide an outstanding addition to their teaching toolkit by using this digital math manipulative. They can not only provide directed exploration opportunities for students but also allow their learners to develop a solid understanding of mathematics concepts that involve algebra. These engaging and dynamic algebra tiles math manipulatives will assist students in demonstrating and sharing their knowledge of how to solve simple and complex algebra concepts. Students will not only understand algebra but also develop a richer and more complex understanding of counting, area, perimeter, and arithmetic, as well as equations, factoring quadratics, algebraic long division, and simultaneous equations. Use Oryx Learning virtual algebra tiles digital math manipulatives to help clarify misconceptions and build connections between concepts and representations.