Finding The Mean Absolute Deviation
Concept
Calculate the mean absolute deviation of a given set of data.
Mean absolute deviation is an indicator of the spread of the data, or how far each data value is from the mean. The higher the mean absolute deviation, the further spread the data is from the mean.
Rules
Steps to finding mean absolute deviation:
1. Find the mean.
2. Find the absolute value of the differences between each value in the data set and the mean.
3. Find the average of the absolute values of the differences between each value in the data set and the mean.
Example
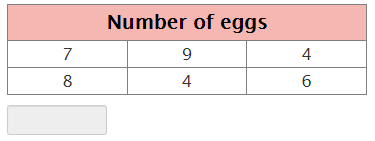
The table below shows the number of calories in different types of cookies. Find the mean absolute deviation of the set of data. Round the final answer to the nearest hundredth.
| Number of Calories in Various Cookies | |||
|---|---|---|---|
| 40 | 50 | 43 | 49 |
| 64 | 22 | 56 | 47 |
Example
The first step in finding the mean absolute deviation is calculating the mean.
Mean (Average) =
Mean (Average) =
Mean (Average) = = 46.375
Next we need to take the absolute value of each data value minus the mean.
│40 – 46.375│ = 6.375 ,
│50 – 46.375│ = 3.625 ,
│43 – 46.375│ = 3.375 ,
│49 – 46.375│ = 2.625 ,
│64 – 46.375│ = 17.625 ,
│22 – 46.375│ = 24.375 ,
│56 – 9.625│= 9.625 ,
│47 – 46.375│= 0.625
Add all of the values together.
6.375 + 3.625 + 3.375 + 2.625 + 17.625 + 24.375 + 9.625 + 0.625 = 68.25
Lastly, to find the mean absolute deviation we take our total and divide it by the number of data values we started with.
Mean absolute deviation = = 8.53125, which we round to 8.53
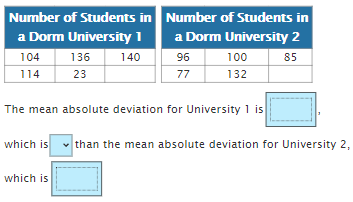
Practice How to Find Mean Absolute Deviation
Practice Problem 1
Drag the correct answer choice in the blank to complete the statement.
Practice Problem 2
The table below shows the number of eggs collected each day at a local household. Find the mean absolute deviation of the data set. Round the final answer to the nearest hundredth.
Practice Problem 3
The two tables below show the number of students in dorms for two different universities. Find the mean absolute deviations and fill in the blanks. Round your answers to the nearest hundredths.
Mean: is the average of the data set.
Range: It is the difference between the highest and lowest values in the set.
Mean absolute deviation: is an indicator of the spread of the data, or how far each data value is from the mean. The higher the mean absolute deviation, the further spread the data is from the mean.
Standard deviation: is a calculated value that shows how the data deviates from the mean of the data.
Pre-requisite Skills