Hypotenuse Leg Theorem
Concept
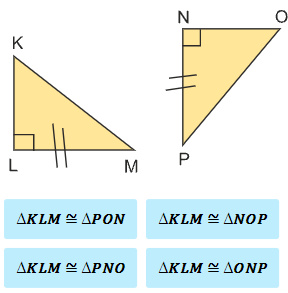
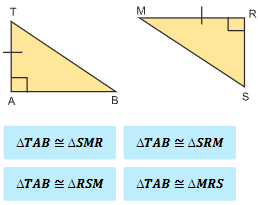
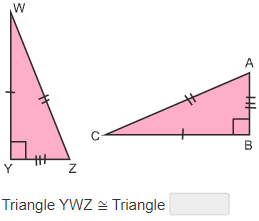
Determine the congruence statement for given two congruent figures using the hypotenuse leg theorem.
Rules
The Hypotenuse-Leg Theorem states that two right triangles are congruent if and only if the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of the other right triangle.
A congruence statement says that two polygons are congruent. To determine a congruence statement, list the corresponding vertices in the same order.
Example
Use the Hypotenuse-Leg Theorem to write the congruent statement for the right triangles below?
Solution
In order to set up a congruence statement, we can write the first figure in whichever order we choose. We can see that the first triangle is named triangle ABC. Now we can match up angles in pairs. We see that the right angle A will match up with the right angle E in the other triangle. Similarly, angle B will pair up with angle F, and angle C will pair up with angle D. Therefore, the congruent statement formed is
|
∆ABC ≅ ∆EFD
|
Practice Hypotenuse Leg Theorem
Practice Problem 1
Which of the following is the correct congruent statement for the right triangles below?
Practice Problem 2
Which of the following is the correct congruent statement for the right triangles below?
Practice Problem 3
The two figures below are congruent. Fill in the blank to make the congruent statement true:
Similar – Figures that have the same shape, but not necessarily the same size.
Congruent – Figures that have the same shape and same size.
Corresponding parts – The parts of congruent figures that match or correspond.
Pre-requisite Skill
Congruence and Transformations