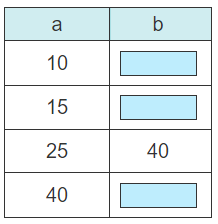
Ratio Tables
Concept
A ratio table is a structured list of equivalent (equal value) ratios that helps us understand the relationship between the ratios and the numbers. Ratios are proportional if they represent the same relationship.
Rules
The order of the values in a ratio relates directly to the order of the quantities described.
To find an equivalent ratio, multiply or divide both quantities by the same number.
To determine whether two ratios are equivalent, write them as simplified fractions. If the fractions are equal, the ratios are equivalent.
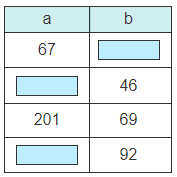
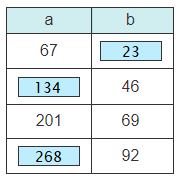
Example
Solution
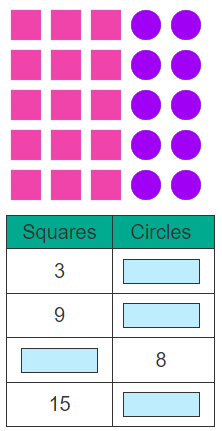
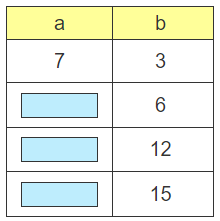
Practice Ratio Tables

A ratio is a comparison of two quantities by division. Ratios describe a part-to-part comparison or a part-to-whole comparison.
Ratio tables show pairs of corresponding values, with an equivalent ratio between each pair.
Equivalent ratios – ratios that have the same value.
Proportional – when two quantities have a constant ratio or unit rate.
Non-proportional – when two quantities don’t have a constant ratio or unit rate.
Pre-requisite Skills
Ratios
Ratios and Fractions
Identify and Write Equivalent Ratio
Related Skills
Identify proportional relationships
Solving Proportions
Ratio Applications
Unit Rate Applications
Proportional Relationships Applications
Unit Rate
Dimensional Analysis
Identifying Proportional Relationships Using a Table
Solving Proportions
Constant Rate of Change
Slope
Direct Variation
Changes in Dimensions