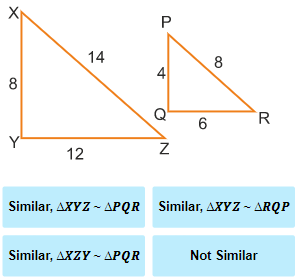
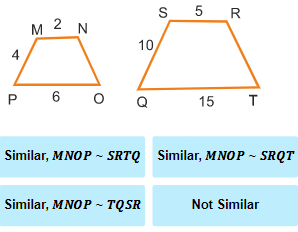
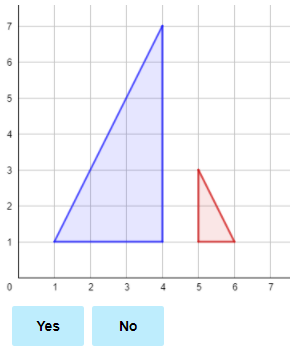
Similarity Statement

Concept

Similarity is an important concept in geometry that helps prove some theorems and their corollaries. The statement of similarity is based on the fact that for two shapes to be similar, they have to have the same angles and their sides have to be in proportion.

Rules

1. Take the corresponding sides of the polygons and set up ratios.
2. If all the ratios are same, the polygons are similar. When two polygons are similar, then their corresponding angles are congruent and the measures of their corresponding sides are proportional. The similarity statement can be found.
3. If all the ratios are not same, the polygons are not similar. The similarity statement cannot be found.
4. To determine the similarity statement, place the corresponding angles in order for both polygons.

Example

Write the similarity statement for the figures below.

Solution

If we take the corresponding sides of the triangles and set up ratios, we would have:
$\fn_phv \frac{10}{15}=\frac{6}{9}=\frac{8}{12}$
All of the ratios reduce to a value of $\fn_phv \frac{2}{3}$ , thus giving us a scale factor of $\fn_phv \frac{2}{3}$ .
The figures are therefore similar, and the similarity statement, placing corresponding angles in order, would be ∆ABC ~ ∆DEF