How Many Solutions Does an Equation Have?
Concept
A system of equations is a set of equations that seek a common solution for the variables included.
Solving a system of equations means finding the values of the variables used in the set of equations. We compute the values of the unknown variables still balancing the equations on both sides. The main reason behind solving an equation system is to find the value of the variable that satisfies the condition of all the given equations true. A system of linear equations usually has a single solution, but sometimes it can have no solution (parallel lines) or infinite solutions (same line).
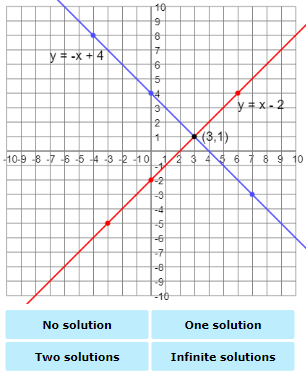
One Solution: The solution to the system will be the point where the two lines intersect.
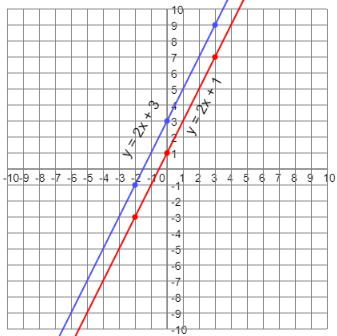
No Solution: If the system of linear equations have the same slope, the lines are parallel and will never intersect. The system will have no solution.
Infinite Solutions: If the two lines have the same y-intercept and the slope, they are actually in the same exact line. The system of linear equations will have infinite solutions.
Rules
Determine if given ordered pairs are solution of the system of linear equations in the form of y = mx + b.
1. To solve, substitute the ordered pairs into both equations.
2. The coordinate point is a solution if it makes both equations true.
3. If the coordinate point does not make both equations true, it is not a solution.
Solve a system of linear equations by graphing:
1. Graph both lines using y-intercept and slopes then find the point of intersection.
2. The point of intersection will be the point where the two lines intersect.
Solve system of linear equations by substitution with one variable isolated:
Step 1: Solve one of the equations for one of the variables.
Step 2: Substitute the expression of the isolated variable in the other linear equation.
Step 3: Solve the equation, and you have one of the coordinates of the intersection.
Step 4: Then plug in the value of the coordinate found in step 2 to either equation to find the other coordinate.
Solve a system of linear equations in standard form by elimination:
The elimination method eliminates one of the variables by adding the equations together.
Step 1: Eliminate one of the variables by adding the equations together.
Step 2: After eliminating one variable, solve for the variable that is left in the equation.
Step 3: After solving for one variable, substitute that value into one of the equations and find the value of the second variable. The values of the two variables is the solution to the system of equations (x, y).
Solve a system of linear equations in standard form by elimination (Multiply one of the equations by a constant):
If adding the equations together does not eliminate a variable, multiply one of the equations by a constant to make a coefficient in each equation be of opposite values.
The elimination method eliminates one of the variables by adding the equations together.
Solve the new system by following the three steps:
Step 1: Eliminate one of the variables by adding the equations together.
Step 2: After eliminating one variable, solve for the variable that is left in the equation.
Step 3: After solving for one variable, substitute that value into one of the equations and find the value of the second variable. The values of the two variables is the solution to the system of equations (x, y).
Example
Solution
The graphs contain the same slope, and so the lines are parallel and will never intersect. The system will have no solution.
Practice How Many Solutions Does an Equation Have?
Practice Problem 3
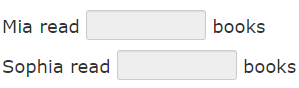
Two classmates have decided to read all the volumes in a popular series of books. Mia has already read 10 volumes and will continue to read new ones at a rate of 2 books per week. Sophia, who has not started reading the series yet, will read 3 books per week. If they continue to read at the same pace, after 4 weeks, will they have read the same number of books?

How many books have each of them read?

Solution: A solution to a system of equations is the value of the variables that make ALL the equations TRUE.
Variable: A symbol, usually a letter, used to represent a number in mathematical expressions or sentences.
Equation: A mathematical sentence stating that two quantities are equal.
System: A system is two or more objects that come together to make a group.
System of Linear Equations: A collection of linear equations involving the same set of variables.
Evaluate – to determine or calculate the numerical value.
Slope intercept form – a linear equation written in the form y = mx + b, where m stands for the slope, and b stands for the y-intercept.
Standard form – a linear equation written in the form Ax + By = C
Eliminate: To remove or cancel out completely.
Intersect: To cross each other.