Geometry Proofs
Concept
Geometric proofs are given statements that prove a mathematical concept is true. In order for a proof to be proven true, it has to include multiple steps. These steps are made up of reasons and statements.
Rules
1. Paragraph proof
Paragraph proofs are comprehensive paragraphs that explain the process of each proof. Like two-column proofs, they have multiple steps and justifications. But instead of columns, the given information is formatted like a word problem — written out in long-hand format.
Paragraph proofs need to be written in chronological order, showing that each step allows the next statement to be true. Each step needs to be supported by a definition, theorem, or postulate.
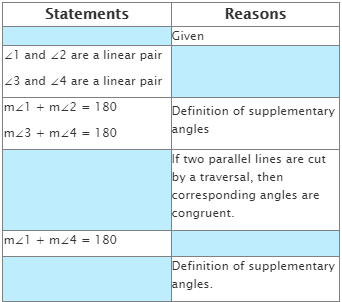
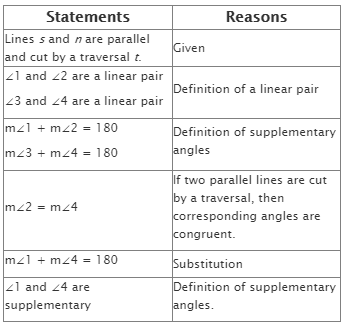
2. Two-column proof
In two-column proofs, the first column has a chronological list of steps. The second column uses deductive reasoning to create a complementary justification for each step. These justifications are either definitions, postulates (assumptions based on mathematical reasoning), or theorems (rules demonstrated through formulas).
1. Start with the given information.
2. Statements with the same reason can be combined into one step.
3 You must have a reason for EVERY statement.
4. The order of the statements in the proof is not always fixed, but make sure the order makes logical sense.
5. Reasons will be definitions, postulates, properties and previously proven theorems. “Given” is only used as a reason if the information in the statement column was given in the problem.
6. Use symbols and abbreviations for words within proofs.
Example
Solution
Practice Geometry Proofs

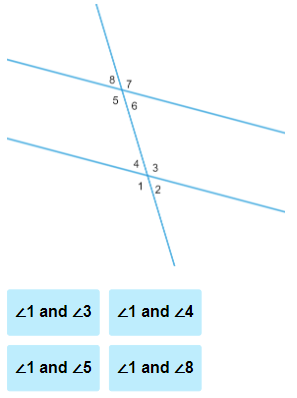
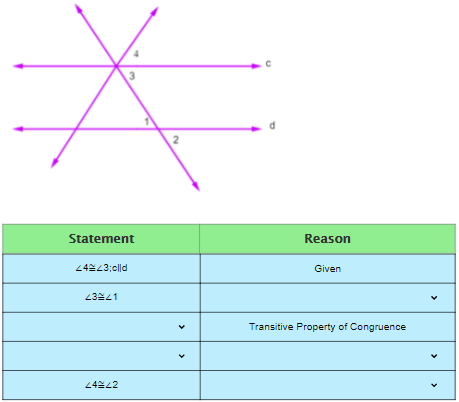
Parallel lines are two or more lines that never intersect.
Transversal line is a line that passes through two lines in the same plane at two distinct points.
Corresponding angles are in the same position relative to the transversal and each of the parallel lines.
Alternate interior angles are on opposite sides of the transversal and between the parallel lines.
Alternate exterior angles are on opposite sides of the transversal and on the outside of the parallel lines.
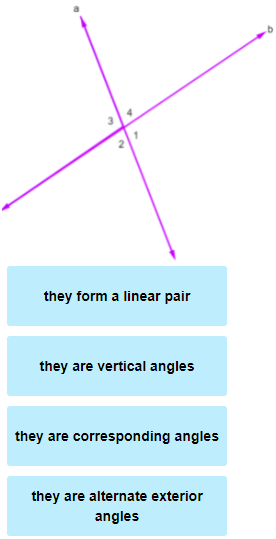
Linear pair: Two adjacent angles whose noncommon sides form a line are a linear pair. The sum of the measures of the angles in a linear pair is 180 degrees.
Vertical angles are two angles that are formed by intersecting lines. They are not adjacent but share a vertex. Vertical angles have the same measure.
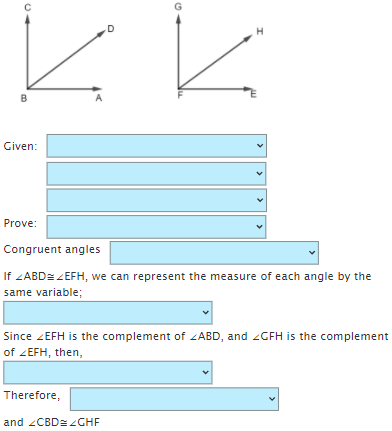
Complementary angles – two angles whose sum is 90 degrees.
Supplementary angles – two angles whose sum is 180 degrees.
Pre-requisite Skills
Angle Relationships
Complementary and Supplementary Angles
Lines
Related Skills
Angles of a Triangle
Polygons and Angles