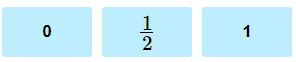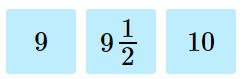Fraction Benchmarks

Concept

In math, benchmark fractions can be defined as common that we can measure or judge against, when measuring, comparing or ordering other fractions.

Benchmark fractions are easy to visualize and identify, and thus, help in estimating the parts. When comparing two fractions with different numerators and denominators, we can either make their denominators common or compare them to a benchmark fraction such as $\fn_phv \frac{1}{2}$ .

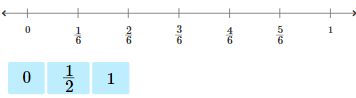
Benchmark fractions are most helpful when fractions to be compared are placed on a number line against the benchmarks.

Rules

To round a fraction to the nearest half:
1. Draw a number line with zero to the far left and the number 1 to the far right.
2. Divide the number line into parts of a whole. The parts are the same as the denominator in the fraction that is being rounded.
3. Number the parts.
4. Find the fraction that is being rounded on the number line.
5. Determine if the fraction is closest to the benchmarks 0, $\fn_phv \frac{1}{2}$ , or 1.
To round a mixed number:
1. Determine what whole numbers the given number is between.
2. Convert the half so it has a common denominator as the fractional part of the given number.
3. Determine if the given number is closer to the lesser whole number, a half, or the greater whole number.
4. Round to the closest number.

Example

Round $\fn_phv {\color{Teal} \frac{7}{8}}$ to the nearest half.

Solution

To round a fraction to the nearest half:
1. Draw a number line with zero to the far left and the number 1 to the far right.
2. Divide the number line into parts of a whole. The parts are the same as the denominator in the fraction that is being rounded. (In this case, divide the number line into 8 parts).

3. Number the parts $\fn_phv {\color{Red} \frac{1}{8}}$ through $\fn_phv {\color{Red} \frac{8}{8}}$ . Notice $\fn_phv {\color{Red} \frac{8}{8}}$ is the same as one whole.
4. Find the fraction that is being rounded on the number line.
5. Determine if the fraction is closest to the benchmarks 0, $\fn_phv \frac{1}{2}$ , or 1.

$\fn_phv {\color{Red} \frac{7}{8}}$ is closest to 1

Practice Fraction Benchmarks

Practice Problem 1

Round $\fn_phv {\color{Teal} \frac{2}{6}}$ to the nearest half.
Use the number line for reference.

Practice Problem 2

Round $\fn_phv {\color{Teal} \frac{4}{7}}$ to the nearest half.

Practice Problem 3

Round $\fn_phv {\color{Teal} 9\frac{5}{11}}$ to the nearest half.

Practice Problem 4

Dahlia needs to bake 15 batches of cookies. She has made 13 so far. About what fraction of the batches of cookies has she made so far?

Practice Problem 5

Bruce has to walk $\fn_phv {\color{Teal} 5\frac{4}{7}}$ meters to reach the nearest bus stop. To the nearest half meter, how much does Bruce have to walk?
Write your answer as a whole number or mixed number in the simplest form.

A fraction is a part of a whole.

Benchmark – a standard or point of reference against which things may be compared.

Fraction Benchmarks – common fractions that we can measure or judge against, when measuring, comparing or ordering other fractions. A benchmark fraction is easy to visualize and helps in estimating the parts of a whole.
The benchmark fractions are 0, $\fn_phv \frac{1}{2}$ , and 1.

Pre-requisite Skills
Fractions – Part of a Whole
Graph Unit Fractions on a Number Line
Comparing Fractions
Read Mixed Number on a Number Line