Volume of Spheres

Concept

The volume of a sphere is the measurement of the space it can occupy. A sphere is a three-dimensional shape that has no edges or vertices.

Rules

Volume of spheres:
The volume V of a sphere is four-thirds the product of π and the cube of the radius r.

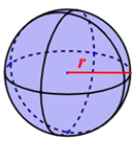
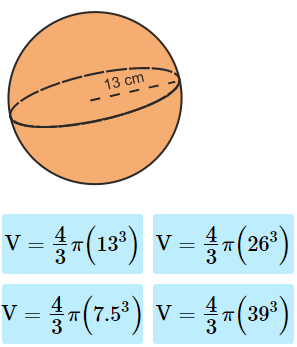
1. Use the formula $\fn_phv V = \frac{4}{3}\pi r^{3}$ to find the volume of the sphere.
2. Substitute in the given value for r.
3. Solve using order of operations.

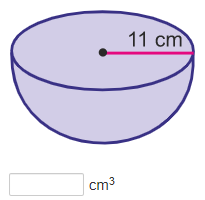
Volume of hemispheres:
The volume of a hemisphere is half the volume of a sphere.

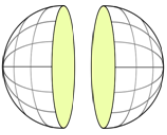
1. First, find the volume of the sphere by using the volume formula: $\fn_phv V = \frac{4}{3}\pi r^{3}$
2. Substitute in the given values for r and solve.
3. Divide the answer by 2 to find the volume of the hemisphere.

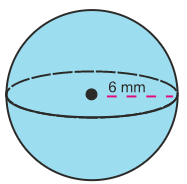
Example

Find the volume of the sphere. Round to the nearest tenth.

Solution

1. Use the formula V = $\fn_phv \frac{4}{3}\pi r^{3}$ to find the volume of the sphere.

2. Substitute r = 6 mm in the given formula.

V = $\fn_phv \frac{4}{3}\pi (6)^{3}$

3. Solve using order of operations.
V = 904.8 mm³

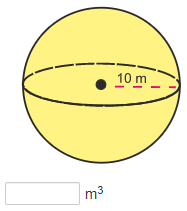
Practice Volume of Spheres

Practice Problem 1

Choose the correct formula to find the volume of the given figure.

Practice Problem 2

Find the volume of the sphere. Round to the nearest tenth.
Use 3.14 for π.

Practice Problem 3

Find the volume of the hemisphere. Round to the nearest tenth.
Use 3.14 for π.

Volume: It is the measure of the space occupied by a solid. Volume is measured in cubic units.

Sphere: A geometrical object in three-dimensional space that is like the surface of a ball. It has a set of all points in space that are a given distance (the radius) from a given point called the center.

Hemisphere: A sphere split in half forms two congruent shapes each called a hemisphere. The face formed by the slice is a circle

Pre-requisite Skills
Volume of Rectangular Prisms
Volume of Prisms
Volume of Cylinders

Geometry and Spatial sense

Volume of Spheres

Volume of Spheres

Practice Problem 1

Practice Problem 2

Practice Problem 3

Menu