Surface Area of Cylinders
Concept
The surface area of a cylinder can be defined as the total space covered by the flat surfaces of the bases of the cylinder and the curved surface. The total surface area of the cylinder has two components:
1. curved surface area
2. flat surface area (of the two flat faces)
The surface area of a cylinder can be defined as the amount of space covered by a flat surface of the base of the cylinder and the curved surface of the cylinder. The surface area of the cylinder is actually the sum of an area of a circle since the base of the cylinder is a circle and the area of curved surface which is a rectangle of length height of the cylinder and circumference of the base as width. Surface area is expressed as the “number of” square units (square centimeters, square inches, square feet, etc.).
Rules
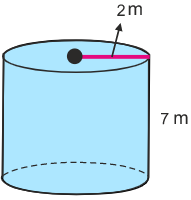
1. Use the formula S.A. = 2πrh + 2πr2 to find the the surface area of a cylinder.
2. Substitute the measurements given into the formula.
3. Use order of operations to solve.
Example
Calculate the surface area of the cylinder shown below.
Solution
1. The surface area of a cylinder is calculated by using the formula.
S.A. = 2πrh + 2πr2
2. Substitute the measurements given into the formula.
S.A. = 2π(2)(7) + 2π(2)2
3. Use order of operations to solve.
S.A. = 87.9645 + 25.13274
S.A = 113 m2
Practice Surface Area of Cylinders
Practice Problem 1
Find the surface area of the cylinder. Round to the nearest whole unit.
Use 3.14 for π.
Practice Problem 2
Simon is covering a battery with plastic wrap. He needs to know how much plastic wrap he should cut to cover the whole battery. If the battery is a cylinder with a height of 1 centimeter and a radius of 5 centimeters, what is the area Simon needs to cover (round to the nearest centimeter)?
Use 3.14 for π.
Practice Problem 3
Verano is covering a candle with paper. He needs to know how much paper he should cut to cover the whole candle. If the candle is a cylinder with a height of 10 centimeters and a radius of 3 centimeters, what is the area Verano needs to cover (round to the nearest centimeter)?
Use 3.14 for π.
Cylinder: A three-dimension figure with two parallel congruent circular bases connected by a curved surface.
Surface area: It is the sum of the areas of all the surfaces of a three-dimensional figure.
Lateral area: It is the surface area of the figure, excluding the area of the base(s) of a three-dimensional figure.
Net: A two-dimensional shape that can be modified to form a three-dimensional shape or a solid. A 3-D shape may have different nets.