What are Faces, Edges and Vertices
Concept
All the objects have a shape. Shapes are either two-dimensional or three-dimensional. A shape that has a length and a width is called a two-dimensional shape (also known as 2-D shape) and a shape that has a length, a width and a height is called a three-dimensional shape (also known as 3-D shape).
A solid shape is a 3-D shape that has 3 dimensions, which are length, width and height (depth).
2-D shapes or Plane figures
2-D shapes are plane geometric figures made up of either straight or curved lines. They only have length and width (breadth). 2-D shapes do not have any depth. Circles, triangles, squares and rectangles are some examples of 2-D shapes. Shapes that are made up of three or more straight lines are referred to as ‘Polygons’. Some common 2-D shapes are circle, oval, triangle, square, diamond, rhombus, parallelogram, rectangle.
3-D shapes or Solid shapes
A 3-D shape or a solid shape has a length, width and height. A solid shape occupies some space and rests on one or more surfaces. Cubes, cones, spheres, cuboids are some examples of solid shapes. Some of the 3-D shapes are cuboid, sphere, cone, cylinder, pyramid, cube.
Rules
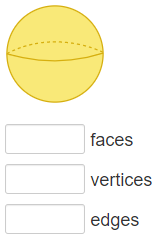
All solid shapes are defined by a certain number of faces, vertices and edges.
Faces:
Every single surface of a solid shape is called a face.
Vertices:
In a solid shape, a ‘Vertex’ is defined as a point where two or more lines meet. Vertices is the plural form of the word ‘Vertex’.
Edges:
In a solid shape, an ‘Edge’ is defined as a line segment joining two vertices or two corners.
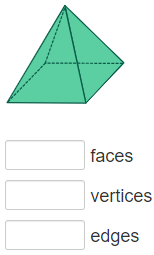
Example
Solution
This 3D solid has 5 faces, 8 edges, and 5 vertices.
Practice What are Faces, Edges and Vertices

3D shapes – 3D shapes are 3-dimensional solid shapes. They have 3 dimensions – length, width and height.
A face is a flat surface.
An edge is where two faces meet.
A vertex is a corner where edges meet. The plural is vertices.