Adding Algebraic Expressions Word Problems

Concept

In mathematics, just like we add many numbers as we can and find the sum, we add two or many algebraic expressions too. However, for the addition of algebraic expressions, we combine all the like terms and then add them.

Like terms are the terms that have the same power for the same variables. In like terms, one can only change the numerical coefficient. Terms that have different variables or the same variables raised to different powers are known as, unlike terms.

Word problems that include addition of algebraic expressions can be solved with ease if we know how to add them. We need to write out an algebraic expression that we can evaluate to find our answer. To write our algebraic expression, we carefully read the problem to figure out what our important numbers are and what kind of operation we are dealing with.

Rules

There are two methods to do the addition of algebraic expressions:
Horizontal method of Addition of Algebraic Expressions
Column method for Addition of Algebraic Expressions

Horizontal method of Addition of Algebraic Expressions
1. Write all the expressions in a horizontal line by putting them into brackets and put an addition sign in between.
2. Group all the like terms together from all the expressions and rewrite the expression so formed.
3. Add numerical coefficients of all the like terms followed by the common variable.
4. Rewrite the simplified expression, and make sure all the terms in the final answer should be unlike terms.

Column method for Addition of Algebraic Expressions
1. Write all the expressions one below the other. Make sure to like terms in one column. If there a term whose like term is not there in the second expression, then either write below it or leave that column blank.
2. Add the numerical coefficient of each column (like terms) and write below it in the same column followed by the common variable.

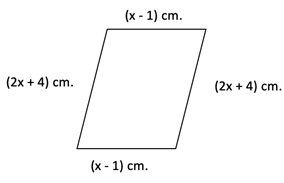
Example

Write a linear expression in simplest form to represent the perimeter of the rhombus. Then find the perimeter if x = 5 centimeters.

Solution

We know that the perimeter of a rhombus p = 2l + 2w

p = 2(x – 1) + 2(2x + 4)
p = (2x – 2) + (4x + 8)
p = 6x + 6

When x = 5, the perimeter will be:

p = 6x + 6
6(5) + 6 = 36

Linear expression in simplest form: p = 6x + 6
Perimeter = 36 cm

Practice Adding Algebraic Expressions Word Problems

Practice Problem 1

Susan is 5x – 2 years old. Her brother Mark is (-x + 1) years older than Susan. Their father Kevin is 7 times as old as Mark. Simplify the expression that represents Kevin’s age. Then find the number that represents Kevin’s age if x = 2.

Practice Problem 2

Robert bought 3 chocolates at (x + 1) dollars each, and 2 cupcakes at (2x – 5) dollars each. Simplify the expression. Then find the total cost if x = 5.

Practice Problem 3

Write a linear expression in simplest form to represent the perimeter of the triangle. Then find the perimeter if x = 3.6 centimeters, rounded to the nearest tenth.

Math Vocabulary

Linear Expression – an algebraic expression in which the variable is raised to the first power, and variables are not multiplied or divided.

Term – either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or − signs.

Like terms – Terms that have the same power for the same variables. In like terms, one can only change the numerical coefficient.

Unlike terms – Terms that have different variables or the same variables raised to different powers.

Distributive Property – to multiply a sum or difference by a number, multiply each term inside the parenthesis by the number outside the parenthesis.

Constant – a term without a variable.

Variable – In algebra, a symbol (usually a letter) standing in for an unknown numerical value in an equation or expression.

Coefficient – is an integer that is multiplied with the variable of a single term or the terms of a polynomial.

Pre-requisite Skills
Evaluate Variable Expressions-addition and subtraction
Evaluate Expressions (Multiplication and Division)
Solve Algebraic Equations – Addition and Subtraction
Solve Algebraic Equations – Multiplication and Division
Evaluate Algebraic Expressions
Write Algebraic Expressions
Arithmetic Sequences
Geometric Sequences
The Distributive Property
Simplifying Complex Algebraic Expressions