Interior Angles in Regular Polygons
Concept
Rules
1. To find the measure of one interior angle in a regular polygon, first find the sum of interior angles of the required polygon using the formula given below.
Sum of interior angles = (n – 2) ∙ 180°
2. Next, divide the sum of interior angles by the total number of angles the regular polygon has.
Example
Solution
To find the measure of one interior angle in a regular polygon, first find the sum of interior angles of the required polygon using the formula given below.
Sum of interior angles = (n – 2) ∙ 180°
A decagon has 10 sides, so:
(10 – 2) ∙ 180 = 8 ∙ 180° = 1,440°
Since this is a regular decagon, all of the angles are equal, so divide the sum of the interior angles by 10.
Practice Interior Angles in Regular Polygons

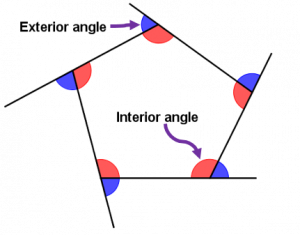
Polygon – A closed figure formed by three or more segments called sides.
Interior angle – An angle of a polygon formed by two of its side and is inside the polygon.
Exterior angle – An angle formed by one side and the extension of the adjacent side. It is outside the polygon.
Related Skill
Geometric Proof