Interior and Exterior Angles of Regular Polygons Word Problems
Concept
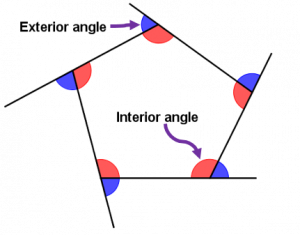
The angles that lie inside a shape, generally a polygon, are said to be interior angles.
An exterior angle of a polygon is the angle that is formed between any side of the polygon and a line extended from the next side. Every polygon has interior and exterior angles. The exterior is the term opposite to the interior which means outside. Therefore exterior angles can be found outside the polygon. The sum of the exterior angles of any polygon is equal to 360°. Any flat shape or figure is said to have interior or exterior angles only if it is a closed shape.
Rules
To find the sum of all interior angles in a regular polygon:
The sum of the interior angles of a polygon can be found by taking the number of sides (n) and subtracting 2. Then, multiply that number by 180.
Sum of interior angles = (n – 2) ∙ 180°
To find the measure of each interior angle in a regular polygon:
1. To find the measure of one interior angle in a regular polygon, first find the sum of interior angles of the required polygon using the formula given below.
Sum of interior angles = (n – 2) ∙ 180°
2. Next, divide the sum of interior angles by the total number of angles the regular polygon has.
To find the measure of each exterior angle in a regular polygon:
The measure of one of the exterior angles of a regular polygon can be found by dividing 360 degrees by the number of angles (n).
Example
Solution
To find the measure of one interior angle in a regular polygon, first find the sum of interior angles of the required polygon using the formula given below.
Sum of interior angles = (n – 2) ∙ 180°
A hexagon has 6 sides, so:
(6 – 2) ∙ 180 = 4 ∙ 180 = 720°
Since this is a regular hexagon, all of the angles are equal, so divide the sum of the interior angles by 6.
Practice Interior and Exterior Angles of Regular Polygons Word Problems

Polygon – A closed figure formed by three or more segments called sides.
Interior angle – An angle of a polygon formed by two of its side and is inside the polygon.
Exterior angle – An angle formed by one side and the extension of the adjacent side. It is outside the polygon.
Related Skill
Geometric Proof