Dividing Integers Using Integer Chips
Concept
An integer is defined as a number that can be written without a fractional component. For example, 11, 8, 0, and −1,908 are integers whereas √5, Π are not integers. The set of integers consists of zero, the positive natural numbers, and their additive inverses.
The division of integers is one of the basic operations performed on integers. Division of integers means equal grouping or dividing an integer into a specific number of groups.
When modeling integers, we can use colored chips to represent these integers. One color can represent a positive number and another color can represent a negative number. Here, a yellow chip will represent a positive integer and a red chip will represent a negative integer.
Rules
Case 1: Dividing two positive integers
1. Use yellow integer chips to represent as many counters as indicated by the first number.
2. Divide the set of chips equally into groups specified by the second number.
Case 2: Dividing two negative integers
1. Use red integer chips to represent as many counters as indicated by the first number.
2. Divide the set of chips equally into groups specified by the second number.
3. Inverse the groups created as negative groups are the opposite of positive groups.
Case 3: Dividing one positive and one negative integer.
i. If the first number is positive and second is negative:
1. Use yellow integer chips to represent as many counters as indicated by the first number.
2. Divide the set of chips equally into groups specified by the second number.
3. Inverse the groups created as negative groups are the opposite of positive groups.
ii. If the first number is negative and second is positive:
1. Use red integer chips to represent as many counters as indicated by the first number.
2. Divide the set of chips equally into groups specified by the second number.
Example
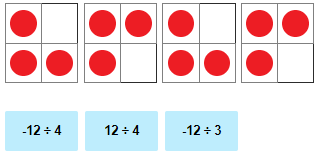
Divide.
-10 ÷ 2
Solution
1. Use red integer chips to represent as many counters as indicated by the first number.
2. Divide the set of chips equally into groups specified by the second number.
-10 ÷ 2 = -5.
Practice Dividing Integers Using Integer Chips
Practice Problem 1
Select the expression that is modeled below.
Practice Problem 2
Select the expression that is modeled below.
Practice Problem 3
Select the expression that is modeled below.
An integer is a number with no decimal or fractional part, from the set of negative and positive numbers, including zero.
Positive Integers: An integer is positive if it is greater than zero. Example: 1, 2, 3 . . .
Negative Integers: An integer is negative if it is less than zero. Example: -1, -2, -3 . . .
Absolute value – the positive distance that a number is from 0 on a number line.
Additive inverses – two integers that are opposites.
Opposites – two integers that are the same distance from 0 on a number line but in opposite directions, like -5 and 5.
Integer chips – Are colored chips with signs. One color represents a positive number and another color represents a negative number.