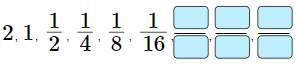Geometric Sequences
Concept
A geometric progression or a geometric sequence is a sequence where every term bears a constant ratio to its preceding term. Geometric progression is a special type of sequence. In order to get the next term in the geometric progression, we have to multiply with a fixed term known as the common ratio, every time, and if we want to find the preceding term in the sequence, we just have to divide the term with the same common ratio.
The geometric progressions can be a finite series or an infinite series. The common ratio of a geometric progression can be a negative or a positive integer.
Rules
1. In an arithmetic sequence, each term is found by adding the same number to the previous term.
2. In a geometric sequence, each term is found by multiplying the same number to the previous term.
Example
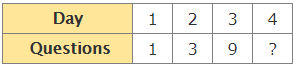
Find the missing number in the sequence.
0.03, _______ , 0.12, 0. 24
Solution
Each term in the pattern is multiplied by 2.
0.03 x 2 = 0.06
Practice Geometric Sequences

Algebraic Expression – an expression that contains variables, numbers, and at least one operation.
Term – each number in a sequence.
Arithmetic Sequence – each term is found by multiplying the same number to the previous term.
Geometric Sequence – each term is found by adding the same number to the previous term.