How to Find Exterior Angles of Triangles Word Problems

Concept

When any side of a triangle is extended, the angle that is formed with this side and its adjacent side is called the exterior angle of a triangle. There are three exterior angles in a triangle. It should be noted that each exterior angle forms a linear pair with its corresponding interior angle. We know that the interior angle of a triangle is formed inside it where the sides meet at a vertex.

Rules

An interior angle is one of the three angles inside of a triangle.
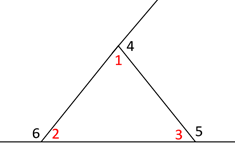
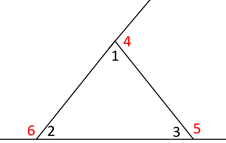
Angles 1, 2, and 3 are interior angles.

An exterior angle is created by extending one side of a triangle beyond the vertex.
Angles 4, 5, and 6 are exterior angles.

The measure of an exterior angle is equal to the sum of the two remote interior angles.
m∠4 = m∠2 + m∠3

There are three basic properties of the exterior angles of a triangle.

i. In a triangle, each exterior angle and its corresponding interior angle form a linear pair of angles. This means that the sum of the interior and exterior angle is equal to 180°.
ii. The exterior angle of a triangle is equal to the sum of the two opposite interior angles (remote interior angles). This is also known as the Exterior Angle theorem.
iii. The sum of all the exterior angles of a triangle is 360°.

Example

A designer is planning to build a bookshelf into the corner of a room. The walls of the room meet at a right angle, and the angle inside the shelf on the right-hand side is 48°. Find the angle that the shelf makes along the left-hand wall.

Solution

The measure of an exterior angle of a triangle is equal to the sum of the remote interior angles.
90° + 48° = 138°

The shelf will make an angle of 138° along the left-hand wall.

Practice How to Find Exterior Angles of Triangles Word Problems

Practice Problem 1

When constructing the roof of a house, the top angle must measure 90 degrees. If the other interior angle measures 45 degrees, what is the measure of the exterior angle the roof makes with the gutter?

Practice Problem 2

A building makes a 90-degree angle with the ground. The man standing on top of that building threw an apple at the bottom of the tree. If we know that the exterior angle from where the apple fell to the tree measures 122 degrees, what was the angle at which the apple was thrown?

Practice Problem 3

Connecting the 3 bases in a baseball field creates a right triangle. If the interior angle at 3rd base is 40 degrees, what is the measure of the exterior angle that 2nd base makes with the foul line?