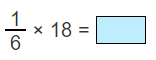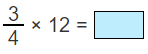Multiples of Fractions
Concept
A fraction represents a part of a whole.
Change the whole number to a fraction
The same process is used when multiplying two or more fractions
Rules
To multiply fractions by a whole number:
1. Change the whole number to a fraction.
2. Simplify the fractions by dividing by their greatest common factor (GCF) one at a time.
3. Reduce them in the simplest form.
4. Multiply the fractions.
5. Rewrite the answer as a mixed number if possible.
Example
Multiply:
Solution
1. Change each number to a fraction.
2. Simplify the fractions by dividing by their greatest common factor (GCF) one at a time.
Divide by 3:
3. Multiply the fractions.
Practice Multiples of Fractions

Numerator – the number above the line in a common fraction showing how many of the parts indicated by the denominator there are.
Denominator – the bottom number in a fraction that shows the number of equal parts an item is divided into. It is the divisor of a fraction.
Proper Fraction – a fraction that is less than one, with the numerator less than the denominator
Improper Fraction – a fraction that is greater than one, with the numerator bigger than the denominator
Like Fractions– fractions with denominators that are same.
Unlike Fractions– fractions with denominators that are different.