Surface Area of Composite Figures
Concept
A composite solid is a solid that is composed, or made up of, two or more solids. The solids that it is made up of are generally prisms, pyramids, cones, and cylinders. In order to find the surface area of a composite solid, you need to know how to find the surface area of prisms, pyramids, cones, and cylinders.
To find the surface area of a composite 3D figure, add the areas of each geometric figure making up the composite 3D figure.
Rules
1. Separate the composite figure into all of its faces. Remember that there is no face where two figures join.
2. Find the area of each individual face.
3. Add all of the areas together.
4. Write the total surface area with the appropriate square units.
Example
Solution
The top pyramid has two surfaces that are triangles with a height of 7 m and a base of 4 m.
Its other two triangular surfaces have a height of 7 m and a base of 5 m.
+
= 63 m2 for the top.
The bottom pyramid has two surfaces that are triangles with a height of 9 m and a base of 4 m.
Its other two triangular surfaces have a height of 9 m and a base of 5 m.
+
= 81 m2 for the top.
The total surface area is 63 m2+ 81 m2 = 144 m2.
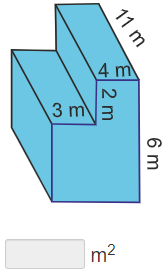
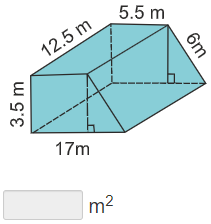
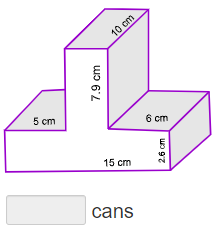
Practice Surface Area of Composite Figures

Surface area: It is the sum of the areas of all the surfaces of a three-dimensional figure.
Lateral area: It is the surface area of the figure, excluding the area of the base(s) of a three-dimensional figure.
Composite solid – a shape composed of a combination of other 3d solids.