Surface Area of Cones
Concept
The surface area of a cone is the amount of area occupied by the surface of a cone. A cone is a 3-D shape that has a circular base. This means the base is made up of a radius and diameter. The distance between the center of the base and the topmost part of the cone is the height of the cone. Stacking many triangles and rotating them around an axis gives the shape of a cone. As it has a flat base, thus it has a total surface area as well as a curved surface area.
Rules
1. Use the formula L.A. = πrl to find the the lateral area of a cone.
Use the formula S.A. = πrl + πr2 to find the the surface area of a cone where r is the radius and l is the slant height of the cone.
2. Substitute the measurements given into the formula.
3. Use order of operations to solve.
Example
Calculate the surface area of the cone shown below.
Solution
Use the formula S.A. = πrl + πr2 to calculate the surface area of a cone.
Substitute the measurements given into the formula and solve.
S.A. = π(6)(6.2) + π(6)2
Use the order of operations to solve.
S.A. = 116.867 + 113.097
S.A. = 229.964 cm2
S.A = 230.0 cm2 round to nearest tenth.
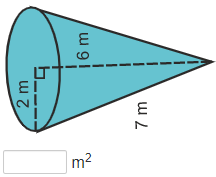
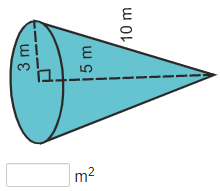
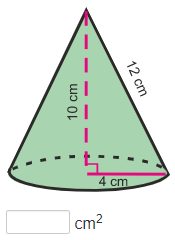
Practice Surface Area of Cones
Practice Problem 1
Calculate the surface area of the cone shown below.
Round to the nearest tenth. Use 3.14 for π.
Practice Problem 2
Calculate the lateral area of the cone shown below.
Round to the nearest tenth. Use 3.14 for π.
Practice Problem 3
Calculate the surface area of the cone shown below.
Round to the nearest tenth. Use 3.14 for π.
Surface area: It is the sum of the areas of all the surfaces of a three-dimensional figure.
Lateral area: It is the surface area of the figure, excluding the area of the base(s) of a three-dimensional figure.
Cone: A three-dimensional figure with one circular base connected by a curved surface to a single vertex.
Slant height – the height of a lateral face.
Net: A two-dimensional shape that can be modified to form a three-dimensional shape or a solid. A 3-D shape may have different nets.