Surface Area of Pyramids

Concept

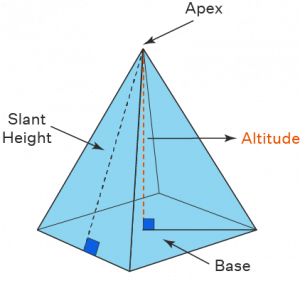
The surface area of a pyramid is obtained by adding the areas of its faces. A pyramid is a three-dimensional shape whose base is a polygon and whose side faces (that are triangles) all meet at a point which is called the apex (or) vertex. The perpendicular distance from the apex to the center of the base is called the altitude or height of the pyramid. The length of the perpendicular drawn from the apex to the base of a triangle (side face) is called the “slant height”.

The surface area of a pyramid is a measure of the total area that is occupied by the surface. In other words, it’s the sum of areas of its faces and hence it is measured in square units such as m², cm², in², ft², etc. A pyramid has two types of surface areas, one is lateral surface area (LSA) and the other is the total surface area (TSA).

The lateral surface area (LSA) of a pyramid = The sum of areas of the side faces (triangles) of the pyramid.
The total surface area (TSA) of a pyramid = LSA of pyramid + Base area.
In general, the surface area of a pyramid without any specifications means the total surface area of the pyramid.

Rules

1. Determine the area of the base (B) and the perimeter of the base (B).
2. Find the slant height (B).
3. Use those values in the formula, $\fn_phv S.A. =B +\frac{1}{2}Pl$
4.State the total surface area in the appropriate square units.

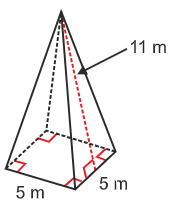
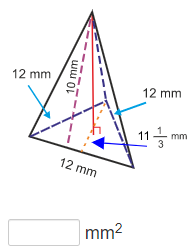
Example

Calculate the surface area of the pyramid shown below.

Solution

$\fn_phv S.A. = Base\;area+\frac{1}{2}(Perimeter)(Length)$

or, $\fn_phv S.A. = B+\frac{1}{2}Pl$

$\fn_phv S.A. = 5^{2}+\frac{1}{2}(4\times5)\times 11$

$\fn_phv S.A. = 25+110$

$\fn_phv {\color{Red} S.A. = 135\;m^{2}}$

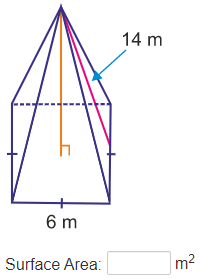
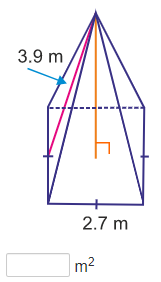
Practice Surface Area of Pyramids

Practice Problem 1

Find the total surface area of the pyramid.

Practice Problem 2

Oliver is making a toybox from wood in the shape of a pyramid. Dimensions are below. How many square meters of wood are needed?
Round your answer to the nearest tenth.