Volume of Cones

Concept

A cone is a three-dimensional shape that has a circular base and it narrows down to a sharp point called a vertex. The volume of a cone is the space occupied by the cone. The formula to find the volume of a cone, whose radius is ‘r‘ and height is ‘h‘ is given as, Volume = $\fn_phv (\frac{1}{3})\pi r^{2}h$ cubic units. Let A = Area of base of the cone and h = height of the cone. Therefore, the volume of cone = $\fn_phv (\frac{1}{3})\times A\times h$ ). Since the base of the cone is of circular shape, we substitute the area to be πr². Volume of cone = $\fn_phv (\frac{1}{3})\pi \times r^{2}\times h$ cubic units. Also, the volume of a cone is one-third of the volume of a cylinder.

Rules

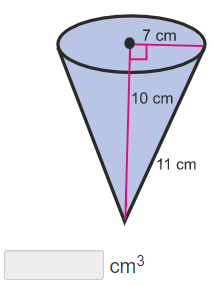
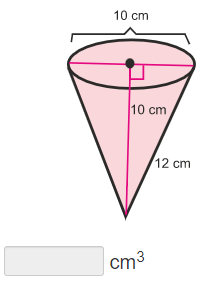
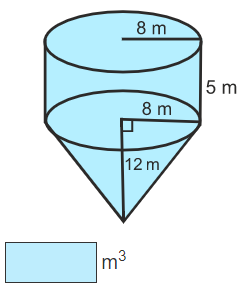
1. Use the formula $\fn_phv V = \frac{1}{3}\pi r^{2} h$ to find the volume of the cone.
2. Substitute in the given values for r and h.
3. Solve using order of operations.

Example

Find the volume of the cone. Round to the nearest tenth.

Solution

1. Use the formula V = $\fn_phv \frac{1}{3}\pi r^{2} h$ to find the volume of the cone.
2. Substitute in the given values for r and h.
h = 6
r = 3
3. Solve using order of operations.
V = $\fn_phv \frac{1}{3}\pi (3)^{2} (6)$
V = 56.5 in³