What is a Proportional Relationship

Concept

A proportional Relationship is a statement that two ratios are equal. It can be written in two ways: as two equal fractions $\fn_phv \frac{a}{b}=\frac{c}{d}$ ; or using a colon, $\fn_phv a:b=c:d$ .

Rules

Identifying proportional relationships through graphs:
To determine whether two quantities are proportional, graph the quantities on a coordinate plane. If the graph of the two quantities is a straight line through the origin, then the two quantities are proportional.

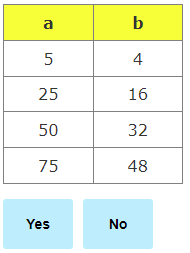
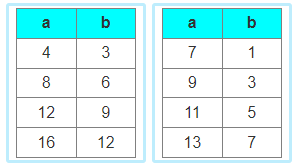
Identifying proportional relationships through tables:
Write the ratios as fractions and then reduce them.
If the reduced fractions are the same, the ratios are proportional.

Example

Samuel rode 5 km in a car and then jogged 8 km per hour. The table below shows how many km he traveled for the number of hours given.
Is the number of km he traveled proportional to the time he traveled?

Solution

Determine if the total distance is proportional to the time.
Write the relationship of the total distance with added hours as a fraction. If proportional, the fractions will be equivalent.
The ratios are not equal, so the number of km traveled is not proportional to the time.

Answer: No

Practice What is a Proportional Relationship

Practice Problem 1

In the following table, are a and b in a proportional relationship?

Practice Problem 2

Select all the tables which show a and b in a proportional relationship.

Practice Problem 3

A plant is 15 cm tall after 1 week, 30 cm tall after two weeks, 46 cm tall after three weeks, and 60 cm tall after week four. Is the plant’s growth proportional to the number of weeks it grew?

Practice Problem 4

On average, Ralph walks at a speed of about 2 meters per second. Graph the relationship between the distance walked and the time spent walking. Is the relationship proportional?