What is the Constant of Proportionality
Concept
Constant of proportionality is the constant value of the ratio between two proportional quantities. Two varying quantities are said to be in a relation of proportionality when, either their ratio or their product yields a constant. The value of the constant of proportionality depends on the type of proportion between the two given quantities: Direct Variation and Inverse Variation.
Direct Variation: The equation for direct proportionality is y = kx, which shows as x increases, y also increases at the same rate.
Inverse Variation: The equation for the indirect proportionality is y = , which shows that as y increases, x decreases and vice-versa.
In both the cases, k is constant. The value of this constant is called the coefficient of proportionality. The constant of proportionality is also known as unit rate.
Rules
1. In a direct variation equation, the constant rate of change, or slope, is assigned a special variable, k.
2. Direct variation can be represented by the equation: y = kx, where k ≠ 0
3. When a relationship varies directly, the graph of the function will always go through the origin (0,0).
Example
Determine if the linear relationship is a direct variation. If so, state the constant of proportionality.
Solution
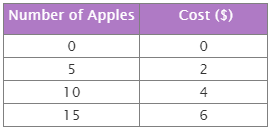
The function shows the relationship between the number of apples(x) and the total cost (y). Use the direct variation equation to see if the relationship is a direct variation.
Compare to the direct variation equation:
to
Ans: Yes,
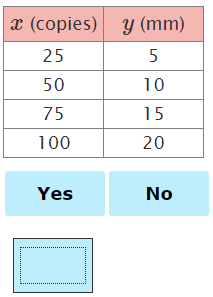
Practice What is the Constant of Proportionality
Practice Problem 1
Determine if the equation is a direct variation. If so, state the constant of variation.
Practice Problem 2
Determine if the linear relationship is a direct variation. If so, state the constant of proportionality.
Write your answer as a whole number or a reduced fraction.
Practice Problem 3
Write the direct variation equation that models the situation.
Jerome builds gift boxes. He builds 5 boxes in 24 seconds. After 38.4 seconds, he has 8 boxes.
x = boxes and y = seconds
Practice Problem 4
y varies directly with x. Find the value of the variable.
y = 910 when x = 5. Find x when y = 546
The constant of proportionality is the ratio between two directly proportional quantities.
Proportional – when two quantities have a constant ratio or unit rate.
Direct Variation – a relationship between two variable quantities with a constant ratio.
A rate is a ratio that compares two quantities with different kinds of units.
A unit rate is a rate that is simplified so that it has a denominator of 1 unit.