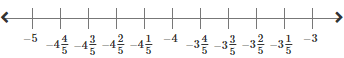X on a Number Line
Concept
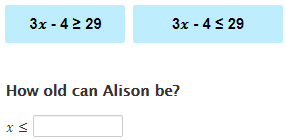
Solve an inequality to find the value of x on the number line.
Rules
1. Use the properties of inequalities to isolate the variable on one side of the inequality.
2. Simplify the other side of the inequality.
3. If the inequality is < or >, put an open circle on the number line at the indicated value. If the inequality is ≤ or ≥, put a filled circle on the number line at the indicated value.
4. Draw a ray in the appropriate direction indicated by the inequality symbol. If < or ≤, then arrow goes to the left, if > or ≥, then arrow goes to the right.
Example
Solution
Practice X on a Number Line

Inequality – a mathematical sentence that compares quantities.
Two-step inequality – an inequality that involves two operations
Addition Property of Inequality – when you add the same number to both sides of an inequality, the inequality remains true.
Subtraction Property of Inequality – when you subtract the same number from both sides of an inequality, the inequality remains true.
Multiplication Property of Inequality – when you multiply by the same number on both sides of an inequality, the inequality remains true.
Division Property of Inequality – when you divide by the same number on both sides of an inequality, the inequality remains true.